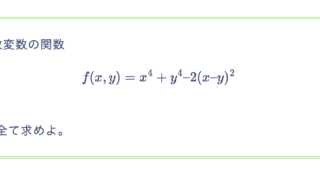行列 $A$ を
\begin{eqnarray}
A =
\begin{bmatrix}
3 & 1 \\
1 & 3 \\
\end{bmatrix}
\end{eqnarray}
とするとき、${\rm exp}(A)$ を求めよ。
なお、行列の指数関数は
\begin{align}
{\rm exp}(A) \equiv \sum_{k = 0}^{\infty} \frac{A^n}{n!}
\end{align}
で定義されるものとする。
\begin{align}
{\rm det}(A -\lambda E_2) &= (3 – \lambda)^2 – 1 \\
&= (2 – \lambda) (4 – \lambda)
\end{align}
となり、これより、固有値は $\lambda = 2, 4$ の2つであることが分かる。ここに、$E_2$ は2行2列の単位行列である。
各々の固有値に対する規格化された固有ベクトルを求めると、
$\lambda = 2$ のとき
\begin{align}
\begin{bmatrix}
\frac{1}{\sqrt{2}} \\
– \frac{1}{\sqrt{2}} \\
\end{bmatrix}
\end{align}
と選ぶことが出来て、また
$\lambda = 4$ のとき
\begin{align}
\begin{bmatrix}
\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} \\
\end{bmatrix}
\end{align}
と選ぶことが出来る。
固有ベクトルの選び方は一意的では無いことに注意して欲しい。固有ベクトルの大きさも1である必要はないが、以下の議論で、単位ベクトルとなるように選んでおくと、計算が簡便になる。
これより、行列 $P$ を
\begin{align}
P &=
\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
– \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\end{bmatrix}
\end{align}
と置けば
\begin{align}
A P &= P
\begin{bmatrix}
2 & 0 \\
0 & 4 \\
\end{bmatrix}\\
A &= P
\begin{bmatrix}
2 & 0 \\
0 & 4 \\
\end{bmatrix}
{}^{\rm t}P
\end{align}
が成り立つことが分かる。
ここに行列 $P$ は $P {}^{\rm t}P = {}^{\rm t}P P = E_2$ を満たしており、直交行列であることを使った。
（これが固有ベクトルを単位ベクトルに取ったご利益である。）
従って、$n=0, 1, 2, \cdots$ に対して
\begin{align}
A^n &= \left(P
\begin{bmatrix}
2 & 0 \\
0 & 4 \\
\end{bmatrix}
{}^{\rm t} P\right)
\left(P
\begin{bmatrix}
2 & 0 \\
0 & 4 \\
\end{bmatrix}
{}^{\rm t} P\right)
\cdots
\left(P
\begin{bmatrix}
2 & 0 \\
0 & 4 \\
\end{bmatrix}
{}^{\rm t} P\right) \\
&=P
\begin{bmatrix}
2 & 0 \\
0 & 4 \\
\end{bmatrix}
\left(P{}^{\rm t}P\right)
\begin{bmatrix}
2 & 0 \\
0 & 4 \\
\end{bmatrix}
\left({}^{\rm t}P P\right)\cdots
\left({}^{\rm t}P P\right)
\begin{bmatrix}
2 & 0 \\
0 & 4 \\
\end{bmatrix}
{}^{\rm t} P \\
&= P
\begin{bmatrix}
2 & 0 \\
0 & 4 \\
\end{bmatrix}^n
{}^{\rm t}P \\
&= P
\begin{bmatrix}
2^n & 0 \\
0 & 4^n \\
\end{bmatrix}
{}^{\rm t}P
\end{align}
となることが分かる。従って
\begin{align}
{\rm exp}(A) &=
\sum_{k = 0}^{\infty} \frac{1}{n!}A^n \\
&= \sum_{k = 0}^{\infty} \frac{1}{n!} P
\begin{bmatrix}
2^n & 0 \\
0 & 4^n \\
\end{bmatrix}
{}^{\rm t}P \\
&= P\left(
\sum_{k = 0}^{\infty}
\frac{1}{n!}
\begin{bmatrix}
2^n & 0 \\
0 & 4^n \\
\end{bmatrix}
\right)
{}^{\rm t} P \\
&=P
\begin{bmatrix}
{\rm e}^2 & 0 \\
0 & {\rm e}^4 \\
\end{bmatrix}
{}^{\rm t} P \\
&=
\begin{bmatrix}
\frac{1}{2}({\rm e}^2 + {\rm e}^4) & \frac{1}{2}(- {\rm e}^2 + {\rm e}^4) \\
\frac{1}{2}(- {\rm e}^2 + {\rm e}^4) & \frac{1}{2}({\rm e}^2 + {\rm e}^4) \\
\end{bmatrix}
\end{align}
と求まる。
