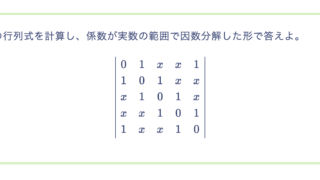
2変数関数\(f(x, y) = \cos(x y)\)について、次の問いに答えなさい。
(1) 全微分\({\rm d} f\)を求めなさい。
(2) \(xyz\)空間内の曲面\(z = f(x, y)\)について、曲面上の点\((x, y, z) = (1, \frac{\pi}{2}, 0)\)における接平面の方程式を求めなさい。
(1)
\[\begin{align}
{\rm d} f &= \frac{\partial f}{\partial x} {\rm d} x + \frac{\partial f}{\partial y} {\rm d} y \\
&= – y \sin(x y) {\rm d} x – x \sin(x y) {\rm d} y
\end{align}\]
\[\begin{align}
{\rm d} f &= \frac{\partial f}{\partial x} {\rm d} x + \frac{\partial f}{\partial y} {\rm d} y \\
&= – y \sin(x y) {\rm d} x – x \sin(x y) {\rm d} y
\end{align}\]
(2)
(1) の結果から、曲面上の点\((1, \frac{\pi}{2}, 0)\)における2つの一時独立な接ベクトルは
\[\begin{align}
\vec{u}_1 &= (1, 0, – \frac{\pi}{2} \sin(1\cdot\frac{\pi}{2})) \\
\vec{u}_2 &= (0, 1, – 1 \sin(1\cdot\frac{\pi}{2}))
\end{align}\]
である。
従って、この点における接平面の法線ベクトル\(\vec{v}\)は
\[
\vec{v} = \vec{u}_1 \times \vec{u}_2 = (\frac{\pi}{2}, 1, 1)
\]
と求まる。
従って、この点における接平面の方程式は
\[\begin{align}
\frac{\pi}{2}(x – 1) + (y – \frac{\pi}{2}) + (z – 0) &= 0 \\
\frac{\pi}{2} x + y + z &= \pi
\end{align}\]
と求まる。