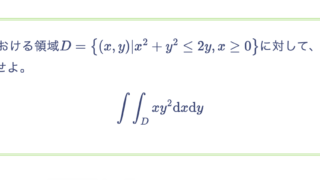を標準化された2次モーメントという。このとき、次の図形の各々について、標準化された2次モーメントを求めよ。
(1) 立方体
(2) 球
(3) 正八面体
(1) 立方体の重心は明らかに立方体の中心なので、立方体の中心を座標の原点にとる。すなわち
このとき、2次モーメント
と求まる。
このとき、2次モーメント
と求まる。
(2) 球の重心は明らかに球の中心であるので、球の中心を原点にとり、極座標で計算を行う。半径
と求まる。
(3) 正八面体の重心は明らかに正八面体の中心であるので、正八面体の中心を原点にとる。一辺の長さが
また、
従って、求めるべき2次モーメント
と求まる。
計算の際に
という風に