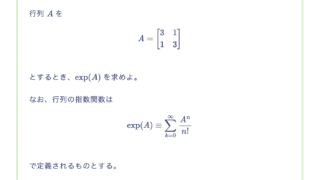
2つの実数変数の関数
の極値を全て求めよ。
2変数関数
である。これらの偏微分を実際に行えば
が得られ、
を満たす
である。これらの偏微分を実際に行えば
が得られ、
を満たす
この2式から
が得られる。
ここで、
を満たす実数
となり、実数解を持つのは
次に、
なる条件が得られる。
この方程式を解くことにより
が得られる。(複合同順)
先に、得られた原点もこの解に含まれるので、これら3つが極値を持つ候補となる。
先ずは、
となる。
ここで
であり、等号が成立するのは、
関数
最後に、原点において極値を持つかどうかを確かめる。
となるが、これを
一方で、
となり、
従って、原点において
以上の議論により、2変数関数