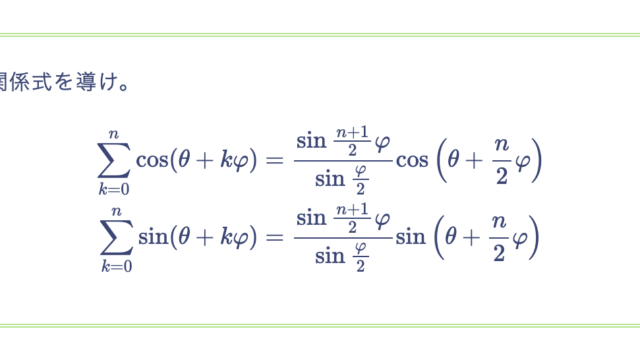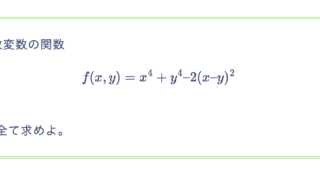次の関数を指定された点 $z = \alpha$ において Taylor 展開せよ。
(1)
\begin{eqnarray}
f(z) &=& \frac{1}{z^2 – 2 z + 3}\ (\alpha = 1)
\end{eqnarray}
(2)
\begin{eqnarray}
f(z) &=& \cos^2 z\ (\alpha = \pi/4)
\end{eqnarray}
(1)
\begin{eqnarray}
f(z) &=& \frac{1}{z^2} \\
f^{(1)}(z) &=& (- 2) \frac{1}{z^3} \\
f^{(2)}(z) &=& (- 2) (- 3) \frac{1}{z^4} \\
f^{(3)}(z) &=& (- 2) (- 3) (- 4) \frac{1}{z^5} \\
f^{(n)}(z) &=& (-1)^n (n + 1)! \frac{1}{z^{n + 2}}
\end{eqnarray}
従って
\begin{eqnarray}
f(z) &=& \sum_{n = 0}^{\infty} \frac{1}{n!} (-1)^n (n + 1)! \frac{1}{2^{n + 2}} (z – 2)^n \\
&=& \sum_{n = 0}^{\infty} (-1)^n \frac{n + 1}{2^{n + 2}} (z – 2)^n
\end{eqnarray}
とテイラー展開出来る。なお、収束半径は$|z – 2| < 2$である。
(2)
\begin{eqnarray}
f(z) &=& \sin z \\
f^{(1)}(z) &=& \cos z \\
f^{(2)}(z) &=& – \sin z \\
f^{(3)}(z) &=& – \cos z \\
f^{(4)}(z) &=& \sin z
\end{eqnarray}
であり、$z = \frac{\pi}{2}$では、$\cos\frac{\pi}{2} = 0, \sin\frac{\pi}{2} = 1$であるので
\begin{eqnarray}
f^{(2 k)}(\frac{\pi}{2}) &=& (-1)^k
\end{eqnarray}
となる。従って
\begin{eqnarray}
f(z) &=& \sum_{n = 0}^{\infty}\frac{(-1)^n}{(2 n)!} \left(z – \frac{\pi}{2}\right)^{2 n}
\end{eqnarray}
とテイラー展開出来る。