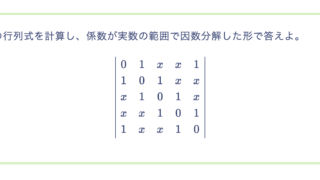
接平面の方程式｜大学・理系（大学数学/大学物理）【レポート代行・課題代行・宿題代行・家庭教師】

2変数関数 $f (x, y) = \cos (x y)$ について、次の問いに答えなさい。

(1) 全微分 $d f$ を求めなさい。

(2) $x y z$ 空間内の曲面 $z = f (x, y)$ について、曲面上の点 $(x, y, z) = (1, \frac{π}{2}, 0)$ における接平面の方程式を求めなさい。

(1)

\begin{aligned} d f & = \frac{\partial f}{\partial x} d x + \frac{\partial f}{\partial y} d y \\ = - y \sin (x y) d x - x \sin (x y) d y \end{aligned}

(2)
(1) の結果から、曲面上の点 $(1, \frac{π}{2}, 0)$ における2つの一時独立な接ベクトルは
$\begin{aligned} {\vec{u}}_{1} & = (1, 0, - \frac{π}{2} \sin (1 \cdot \frac{π}{2})) \\ {\vec{u}}_{2} & = (0, 1, - 1 \sin (1 \cdot \frac{π}{2})) \end{aligned}$
である。

従って、この点における接平面の法線ベクトル $\vec{v}$ は
$\vec{v} = {\vec{u}}_{1} \times {\vec{u}}_{2} = (\frac{π}{2}, 1, 1)$
と求まる。
従って、この点における接平面の方程式は
$\begin{aligned} \frac{π}{2} (x - 1) + (y - \frac{π}{2}) + (z - 0) & = 0 \\ \frac{π}{2} x + y + z & = π \end{aligned}$
と求まる。