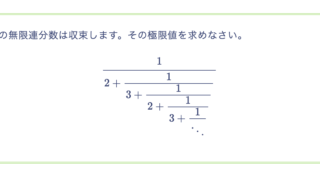
区分求積法｜大学・理系（大学数学/大学物理）【レポート代行・課題代行・宿題代行・家庭教師】

(1) 次の積分を区分求積法によって計算せよ。
$\int_{0}^{1} (x^{2} + x) d x$

(2) 次の関数 $f (x)$ の導関数を求めよ。
$f (x) = \int_{1}^{3 x} (t^{5} + t)^{1} 0 d t$

区間

[0, 1]

を

n

等分し、

x_{0} = 0, x_{1} = 1 / n, x_{2} = 2 / n, \dots, x_{k} = k / n, \dots, x_{n} = 1

とする。
各区間での関数の値を一番左の

x

の値で代表させることにすると、その面積は

\begin{aligned} I_{n} & = \sum_{k = 0}^{n - 1} (x_{k}^{2} + x_{k}) \frac{1}{n} \\ = \frac{1}{n} \sum_{k = 0}^{n - 1} ({(\frac{k}{n})}^{2} + (\frac{k}{n})) \\ = \frac{1}{n^{3}} \sum_{k = 0}^{n - 1} k^{2} + \frac{1}{n^{2}} \sum_{k = 0}^{n - 1} k \\ = \frac{1}{n^{3}} \frac{(n - 1) n (2 n - 1)}{6} + \frac{1}{n^{2}} \frac{(n - 1) n}{2} \end{aligned}

で近似できる。ここで、

n \to \infty

の極限を取ると

\begin{aligned} I & = lim_{n \to \infty} I_{n} \\ = \frac{1}{3} + \frac{1}{2} \\ = \frac{5}{6} \end{aligned}

と求まる。

(2)
$\begin{aligned} \frac{d f (x)}{d x} & = \frac{d}{d x} \int_{1}^{3 x} (t^{5} + t)^{10} d t \\ = 3 \frac{d}{3 d x} \int_{1}^{3 x} (t^{5} + t)^{10} d t \\ = 3 ((3 x)^{5} + 3 x)^{10} \end{aligned}$

区分求積法

2変数関数の極値

Cauchy-Schwarz(コーシー-シュワルツ)の不等式

極限の計算

2変数関数の極値

Cauchy-Schwarz(コーシー-シュワルツ)の不等式

極限の計算

2変数関数の極値

Cauchy-Schwarz(コーシー-シュワルツ)の不等式

極限の計算

カテゴリー