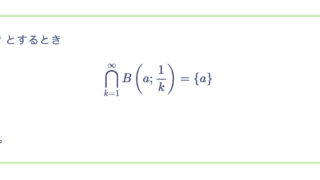$(X, d)$ を距離空間とし、実数値関数 $d’:X \times X \to \mathbb{R}$ を
\begin{align}
d'(x, y) &= {\rm min}\{1, d(x, y)\}\ ((x, y) \in X \times X)
\end{align}
により定める。
(1) このとき、$d’$ は $X$ の距離となることを示せ。
(2) $d$ と $d’$ は $X$ に同じ位相を定めることを示せ。
(1)
$d’$ の正値性と対称性は明らかであるので、三角不等式を満たすことを示せば良い。
$x, y, z \in X$ とするとき、$d(x, y), d(y, z) < 1$ のときは、$d'(x, y) = d(x, y), d'(y, z) = d(x, y)$ であり、
$d'(x, z) = {\rm min}\{1, d(x, z)\} \le d(x, z)$ であるので
\begin{align}
d'(x, z) \le d(x, z) \le d(x, y) + d(y, z) = d'(x, y) + d'(y, z)
\end{align}
より三角不等式が成り立つ。
$d'(x, y) = 1$ のときは
\begin{align}
d'(x, z) = {\rm min}\{1, d(x, z)\} \le 1 \le 1 + d'(y, z) = d'(x, y) + d'(y, z)
\end{align}
となり、やはり三角不等式が成り立つ。$d'(y, z) = 1$ のときも全く同様に示せる。
以上より、$d’$ は三角不等式を満たすことが分かり、$d’$ は $X$ の距離となることが分かる。
(2)
二つの距離 $d, d’$ が $X$ において同じ位相を定めるということは、$d, d’$ によって定められる各々の開集合系が等しいということである。
したがって、$X$ の任意の点列 $\{a_n\}_{n = 1}^{\infty}$ が $d$ に関して $a \in X$ に収束するならば、$d’$ に関して $a$ に収束することと、逆に、$d’$ に関して $a \in X$ に収束するならば、$d$ に関して $a$ に収束することを示せば良い。
先ず、前半を示す。
$\{a_n\}_{n = 1}^{\infty}$ が $d$ に関して $a \in X$ に収束するとすると
\begin{align}
\forall \epsilon > 0, \exists N \in \mathbb{N}, n \ge N \Rightarrow d(a_n, a) < \epsilon
\end{align}
が成り立つ。
今、$d'(a_n, a) \le d(a_n, a)$ であるので、$n \ge N$ に対して $d'(a_n, a) < \epsilon$ となり、数列 $\{a_n\}_{n = 1}^{\infty}$ は $d’$ に関して $a$ に収束することが分かる。
次に後半を示す。
$\{a_n\}_{n = 1}^{\infty}$ が $d’$ に関して、$a \in X$ に収束するとすると
\begin{align}
\forall \epsilon > 0, \exists N \in \mathbb{N}, n \ge N \Rightarrow d'(a_n, a) < {\rm min}\{1, \epsilon\}
\end{align}
が成り立つ。
ここで $n \ge N$ において $d(a_n, a) = d'(a_n, a) < \epsilon$ が成り立つことに注意すると、$d(a_n, a) < \epsilon$ が成り立ち、$\{a_n\}_{n = 1}^{\infty}$ は $a$ に収束する。
以上より、題意が示された。