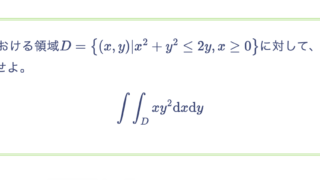3次元図形の2次モーメントの計算

(1) 立方体の重心は明らかに立方体の中心なので、立方体の中心を座標の原点にとる。すなわち\((x_0, y_0, z_0) = (0, 0, 0)\)とする。一辺の長さが\(l\)の立方体を考え、下の領域を考える\(V\)とする。
\[\begin{align}
– \frac{l}{2} \le &x \le \frac{l}{2} \\
– \frac{l}{2} \le &y \le \frac{l}{2} \\
– \frac{l}{2} \le &y \le \frac{l}{2}
\end{align}\]
このとき、2次モーメント\(M\)は、直方体の体積が\(l^3\)である事に注意して
\[\begin{align}
M &= \int\int\int (x^2 + y^2 + z^2) {\rm d}x {\rm d}y {\rm d}z/(3 l^5) \\
&= 3 \int\int\int x^2 {\rm d}x {\rm d}y {\rm d}z/(3 l^5) \\
&= \left[\frac{1}{3}\right]_{- \frac{l}{2}}^{\frac{l}{2}} \cdot \left[y\right]_{-\frac{l}{2}}^{\frac{l}{2}} \cdot \left[z\right]_{-\frac{l}{2}}^{\frac{l}{2}} \\
&= \frac{1}{12}
\end{align}\]
と求まる。

(2) 球の重心は明らかに球の中心であるので、球の中心を原点にとり、極座標で計算を行う。半径\(l\)の球を考えた時、その体積は\(\frac{4}{3} \pi r^3\)に注意して、2次モーメント\(M\)は
\[\begin{align}
M &= \int\int\int (x^2 + y^2 + z^2) {\rm d}x {\rm d}y {\rm d}z /\left(3 \left(\frac{4}{3} \pi l^3 \right)^{\frac{5}{3}} \right) \\
&= \int_0^r r^2 r^2 {\rm d} r \int_0^{\pi} \sin\theta {\rm d}\theta \int_0^{2 \pi} {\rm d}\phi/\left(3 \left(\frac{4}{3} \pi l^3 \right)^{\frac{5}{3}} \right) \\
&= \left[\frac{1}{5} r^5\right]_0^r \cdot \left[-\cos\theta\right]_0^{\pi} \cdot \left[\phi\right]_0^{2 \pi}/\left(3 \left(\frac{4}{3} \pi l^3 \right)^{\frac{5}{3}} \right) \\
&= \frac{1}{5}\left(\frac{3}{4 \pi}\right)^{\frac{2}{3}}
\end{align}\]
と求まる。

(3) 正八面体の重心は明らかに正八面体の中心であるので、正八面体の中心を原点にとる。一辺の長さが\(l\)の正八面体を考え、正八面体の中心を通る面で正八面体の断面が一辺の長さが\(l\)の正方形となる面に\(x-y\)平面をとり、その正八面体の断面の正方形の各頂点が\(\pm\frac{l}{\sqrt{2}}, 0, 0), (0, \pm\frac{l}{\sqrt{2}}, 0)\)となるように\(x\)軸と\(y\)軸をとる。

\(x \leftrightarrow -x, y \leftrightarrow -y, z \leftrightarrow -z\)の入れ替えに対して被積分関数も積分領域も対称なので、\(x \ge 0, y \ge 0, z \ge 0\)において計算し、8倍すれば良い。

また、\(x-y\)平面における積分領域は\(0 \le x \le \frac{l}{\sqrt{2}}, 0 \le y \le \frac{l}{\sqrt{2}} – x\)であり、\(z\)に関しては、正八面体のこの領域での方程式が\(x + y + z = \frac{l}{\sqrt{2}}\)となることから、\(0 \le z \le \frac{l}{\sqrt{2}} – x – y\)となる。

従って、求めるべき2次モーメント\(M\)は、正六面体の体積が\(v = \frac{\sqrt{2}}{3} l^3\)となることに注意して
\[\begin{align}
M &= 8 \int_0^{\frac{l}{\sqrt{2}}} {\rm d}x \int_0^{\frac{l}{\sqrt{2}} – x} {\rm d} y \int_0^{\frac{l}{\sqrt{2}} – x – y} {\rm d} z (x^2 + y^2 + z^2)/(3 v^{\frac{5}{3}}) \\
&= 8 \int_0^{\frac{l}{\sqrt{2}}} {\rm d}x \int_0^{\frac{l}{\sqrt{2}} – x} {\rm d} y \left\{(x^2 + y^2)\left(\frac{l}{\sqrt{2}} – x – y\right) + \frac{1}{3}\left(\frac{l}{\sqrt{2}} – x – y\right)^3 \right\}/(3 v^{\frac{5}{3}}) \\
&= 8 \int_0^{\frac{l}{\sqrt{2}}} {\rm d}x \int_0^{\frac{l}{\sqrt{2}} – x} {\rm d} y \left\{-\frac{4}{3}y^3 + 2\left(\frac{l}{\sqrt{2}} – x\right)y^2 – \left(x^2 + \left(\frac{l}{\sqrt{2}} – x\right)^2\right) y \right.\\
&\ \ \ \ \ \left.+ \left(\frac{l}{\sqrt{2}} – x\right)\left(x^2 + \frac{1}{3}\left(\frac{l}{\sqrt{2}} – x\right)^2\right)\right\}/(3 v^{\frac{5}{3}}) \\
&= 8 \int_0^{\frac{l}{\sqrt{2}}} {\rm d}x \left\{\frac{2}{3}\left(\frac{l}{\sqrt{2}} – x\right)^4 – \frac{\sqrt{2}}{2} l \left(\frac{l}{\sqrt{2}} – x\right)^3 + \frac{l^2}{4}\left(\frac{l}{\sqrt{2}} – x\right)^2\right\}/(3 v^{\frac{5}{3}}) \\
&= 8 \left\{\frac{2}{3}\frac{1}{5}\left(\frac{l}{\sqrt{2}}\right)^5 – \frac{l}{4 \sqrt{2}}\left(\frac{l}{\sqrt{2}}\right)^4 + \frac{l^2}{12}\left(\frac{l}{\sqrt{2}}\right)^3\right\}/(3 v^{\frac{5}{3}}) \\
&= \frac{1}{20}\left(\frac{9}{2}\right)^{\frac{1}{3}}
\end{align}\]
と求まる。