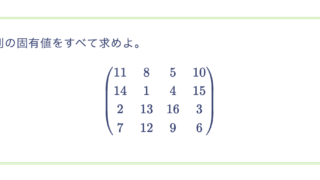
次の級数の和を求めよ。
\[
\sum_{n = 1}^{\infty} \frac{1}{2^n n}
\]
\(|x| < 2\)において収束する次の無限等比級数を考える。
\[
\sum_{n = 1}^{\infty} \left(\frac{x}{2}\right)^n = \frac{x}{2} + \frac{x^2}{2^2} + \frac{x^3}{2^3} + \cdots
\]
この級数は\(|x| < 2\)において次の値に収束する。
\[
\frac{x}{2}\frac{1}{1 – \frac{x}{2}} = \frac{x}{2 – x} = -1 + \frac{2}{2 – x}
\]
この同じ値である2つの式を\(x = 0\)から\(x = 1\)まで積分する。(この積分範囲で級数は収束する。)
最初の級数は
\[\begin{align}
\int_0^1 \sum_{n = 1}^{\infty} \left(\frac{x}{2}\right)^n {\rm d} x &=
\int_0^1 \left(\frac{x}{2} + \frac{x^2}{2^2} + \frac{x^3}{2^3} + \cdots \right) {\rm d} x \\
&= \left[\frac{x^2}{2\cdot 2} + \frac{x^3}{2^2 \cdot 3} + \cdots \right]_0^1 \\
&= \frac{1}{2 \cdot 2} + \frac{1}{2^2 \cdot 3} + \frac{1}{2^3 \cdot 4} + \cdots
\end{align}\]
これに\(\frac{1}{2}\)をかけて\(\frac{1}{2}\)を足せば、求めるべき級数となる。
\[
\frac{1}{2} + \frac{1}{2} \int_0^1 \sum_{n = 1}^{\infty} \left(\frac{x}{2}\right)^n {\rm d} x
= \frac{1}{2 \cdot 1} + \frac{1}{2^2 \cdot 2} + \frac{1}{2^3 \cdot 3} + \cdots
\]
同様の計算を第2式に対して行うと
\[\begin{align}
\frac{1}{2} + \frac{1}{2} \int_0^1 \sum_{n = 1}^{\infty} \left(\frac{x}{2}\right)^n {\rm d} x
&= \frac{1}{2} + \frac{1}{2} \int_0^1 \left(-1 + \frac{2}{2 – x} \right) {\rm d} x \\
&= \frac{1}{2} + \frac{1}{2} \left(-1 + \left[-2 \log(2 – x)\right]_0^1 \right) \\
&= \frac{1}{2} + \frac{1}{2} \left(-1 + 2 \log 2 \right) \\
&= \log 2
\end{align}\]
となり、求める無限級数の和は
\[
\log 2
\]
となる事が示される。
\[
\sum_{n = 1}^{\infty} \left(\frac{x}{2}\right)^n = \frac{x}{2} + \frac{x^2}{2^2} + \frac{x^3}{2^3} + \cdots
\]
この級数は\(|x| < 2\)において次の値に収束する。
\[
\frac{x}{2}\frac{1}{1 – \frac{x}{2}} = \frac{x}{2 – x} = -1 + \frac{2}{2 – x}
\]
この同じ値である2つの式を\(x = 0\)から\(x = 1\)まで積分する。(この積分範囲で級数は収束する。)
最初の級数は
\[\begin{align}
\int_0^1 \sum_{n = 1}^{\infty} \left(\frac{x}{2}\right)^n {\rm d} x &=
\int_0^1 \left(\frac{x}{2} + \frac{x^2}{2^2} + \frac{x^3}{2^3} + \cdots \right) {\rm d} x \\
&= \left[\frac{x^2}{2\cdot 2} + \frac{x^3}{2^2 \cdot 3} + \cdots \right]_0^1 \\
&= \frac{1}{2 \cdot 2} + \frac{1}{2^2 \cdot 3} + \frac{1}{2^3 \cdot 4} + \cdots
\end{align}\]
これに\(\frac{1}{2}\)をかけて\(\frac{1}{2}\)を足せば、求めるべき級数となる。
\[
\frac{1}{2} + \frac{1}{2} \int_0^1 \sum_{n = 1}^{\infty} \left(\frac{x}{2}\right)^n {\rm d} x
= \frac{1}{2 \cdot 1} + \frac{1}{2^2 \cdot 2} + \frac{1}{2^3 \cdot 3} + \cdots
\]
同様の計算を第2式に対して行うと
\[\begin{align}
\frac{1}{2} + \frac{1}{2} \int_0^1 \sum_{n = 1}^{\infty} \left(\frac{x}{2}\right)^n {\rm d} x
&= \frac{1}{2} + \frac{1}{2} \int_0^1 \left(-1 + \frac{2}{2 – x} \right) {\rm d} x \\
&= \frac{1}{2} + \frac{1}{2} \left(-1 + \left[-2 \log(2 – x)\right]_0^1 \right) \\
&= \frac{1}{2} + \frac{1}{2} \left(-1 + 2 \log 2 \right) \\
&= \log 2
\end{align}\]
となり、求める無限級数の和は
\[
\log 2
\]
となる事が示される。