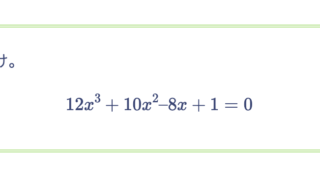整数係数の$n$次代数方程式の有理数解

まず、条件の$a_n\ne 0,a_0\ne 0$について考察する。

$a_n=0$であった場合には、$n–1$次の方程式に帰着するので、この条件により一般性は失わない。
また、$a_0=0$であった場合には、全ての項から$x$をくくり出すことが出来て、やはり$n–1$次の方程式に帰着する。従って、この条件によっても一般性は失わない。

以上の考察から、$a_n\ne 0,a_0\ne 0$と仮定しても一般性は失わないことが分かる。

このとき、与えられた整数係数の$n$次代数方程式が有理数解$\alpha =\frac{p}{q}$を持つとする。
ここで、$q\ne 0,p\ne 0$であり、$p,q$は互いに素であるとする。また、$q>0$としても一般性は失わない。

$p\ne 0$なる条件は、$a_0\ne 0$であるために、$x=0$は解とはなり得ないことから得られる。

$\alpha =\frac{p}{q}$を方程式に代入すると
$$\begin{array}{rl}{a}_n{\left(\frac{p}{q}\right)}^n+a_{n–1}{\left(\frac{p}{q}\right)}^{n–1}+\cdots +a_1\left(\frac{p}{q}\right)+a_0& =0\\ a_n{p}^n+a_{n–1}q{p}^{n–1}+\cdots +a_1{q}^{n–1}p+a_0{q}^n& =0\end{array}$$
が得られる。

ここで
$$\begin{array}{rl}{a}_0{q}^n& =–a_n{p}^n–a_{n–1}q{p}^{n–1}–\cdots –a_1{q}^{n–1}p\\ a_0{q}^n& =p(-a_n{p}^{n–1}–a_{n–1}q{p}^{n–2}–\cdots –a_1{q}^{n–1})\end{array}$$
と変形すると、右辺は$p$の倍数であることが分かる。
一方で、左辺の$q^n$は$p$と$q$が互いに素であるので、$a_0$が$p$の倍数であることが分かる。
言い換えると、$p$は$a_0$の約数である。

さらに、
$$\begin{array}{rl}{a}_n{p}^n& =–a_{n–1}q{p}^{n–1}–\cdots –a_1{q}^{n–1}p–a_0{q}^n\\ a_n{p}^n& =q(-a_{n–1}{p}^{n–1}–\cdots –a_1{q}^{n–2}p–a_0{q}^{n–1})\end{array}$$
と変形することによって、先と同様の議論によって、$a_n$は$q$の倍数である事がわかる。
言い換えると、$q$は$a_n$の約数である。

従って、符合を考慮することにより、題意が示される。