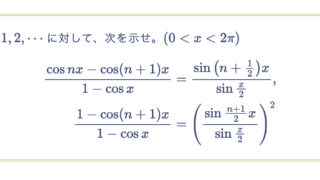
相異なる点
(1) 2点
(2) 3点
(3)
(1) 単に答えを求めるなら
となるが、(2), (3) を見越して、より一般的な方法で導くことにする。
今、求めたい
これを行列で書けば
このような連立1次方程式の解を求める表式はクラメルの公式として知られている。
すなわち
とするとき
と求められる。実際に
となり、これは最初に示した一次式と一致する。
(2) (1) の方法を3行3列の場合に適用することにより
と求まる。ここで
である。
(3) 全く同様の式が
が逆行列を持つかどうかが、一意的に
ここで、
従って、